Abstract: -Multinormed spaces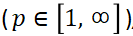present a comparatively new structure of functional analysis. It gradually appeared in papers of quite a few mathematicians. These spaces found important applications in the theory of Banach lattices and some other areas. Also they present an independent interest as a certain ''lighter'' version of quantized normed spaces.

In this talk we give a full description of projective (= homologically best) -multinormed spaces. The result is obtained as a partial case of a result concerning the so-called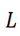-spaces. These are far-reaching generalizations of -multinormed spaces: we get the latter spaces when 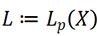, and the measure space with the counting measure.

As a main tool, we use the general-categorical concept of freeness. We introduce and characterize free , defined in terms on some naturally appearing functor. After this, using general-categorical applications of freeness to projectivity, we obtain a broad class of projective . In ``nice'' cases 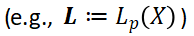the latter happen to be, informally speaking, ``well situated'' complemented subspaces of free spaces.

Abstract: The uniqueness of structure for a separable Banach space is one of the most essential problems in Banach space theory. In 1979, Pelczynski posed the question concerning the symmetric structure of ideals of compact operators on a Hilbert space. Arazy showed that, in order to resolve Pelczynski's question, it suffices to consider isomorphic embeddings of ideals of compact operators. Arazy conjectured that the isomorphic embedding exists if and only if the ideal is . 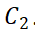In our recent work (Huang, Sadovskaya, Sukochev), we gave an affirmative answer to Arazy's conjecture for a wide class of ideals of compact operators.

Abstract: In this talk I will present some recent progress on the construction of ground states of the honeycomb hubbard model, which is an important model for studying the Fermi liquid-Superconducting phase transitions. Using fermionic cluster expansions and constructive renormalization theory, we proved that the ground state of this model is not a fermi liquid. We also derived the non-perturbative critical temperature for the phase transition. This presentation is based on the joint work with V. Rivasseau: arXiv:2108.10852, arXiv:2108.10415 .

Abstract: There are at least two notions of the algebra of free entire functions (both introduced by J. Taylor in 70s). The question of interest is: what are algebras of free ? We give a partial answer based on the theory of Banach algebras of polynomial growth (over real numbers). Polynomial growth means that for every element 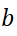the norm of grows more slowly than a polynomial in (here is real). This condition is equivalent to the existence of calculus. Operators of polynomial growth are known since the early 60s but Banach algebras consisting entirely of such operators have not been studied before. We define an enveloping functor w.r.t. this class of Banach algebras and an algebra of free is defined as the result of its application to a free (polynomial) algebra. Interesting algebras are also obtained by applying this functor to universal enveloping and some quantum algebras.

Abstract: The theory of pseudo-differential operators connects partial differential operators with harmonic analysis. It is an important tool in the study of PDE and differential geometry. It has recently been studied by McDonald, Sukochev and Zanin in a C*-algebraic way, which makes it possible to extend the theory to the noncommutative setting. In this talk, I will briefly discuss recent progress of this theory in some noncommutative spaces, mainly on symbol calculus and asymptotic limit of some pseudo-differential operators. Finally I will give an application to Connes' quantum differential and integration in noncommutative geometry.

Abstract: We plan to start from a brief reminding on the classical Kuiper theorem on contractibility of the unitary group of operators on a separable Hilbert space. Then we will discuss its generalizations to the Hilbert C*-module situation. The role of these theorems in K-theory will be presented.

After that we plan to pass to recent results on contactibility of groups of invertibles in algebras which differ from the algeabra of all operators on a Hilbert space/module. More precisely, we will speak about generalized Manuilov's algebra and the uniform Roe algebra with an emphasis on our papers [1,2].

The research is supported by the Russian Science Foundation under grant 21-11-00080.

[1] E. Troitskii. Manuilov Algebra, C*-Hilbert Modules, and Kuiper Type Theorems. Russian J. Math. Phys. 25, 534–544 (2018).

[2] V. Manuilov, E. Troitsky. On Kuiper type theorems for uniform Roe algebras. Linear Algebra Appl., 608, 387-398 (2021).

Abstract: We will discuss some properties of Hilbert C*-modules as generalizations of Hilbert spaces, where some C*-algebra is used instead of the field of complex numbers. It turns out that some natural properties of the classical case in this theory become much more complicated. There exists a well-known characterization of compact operators, and it is well-known that every Hilbert space has a frame. But for the case of Hilbert C*-modules these results without changes are not valid. And the difficulties appear not only because of the more complicated algebraic structure - the module structure, but even for the case of just a commutative C*-algebra. Thus, topological properties become much more important.

Abstract: The celebrated cutoff phenomenon was first discovered by Diaconis and Shahshahani in 1981 for random transpositions, or intuitively for random “card shuffles” : imagine a deck of N cards spread on a table, randomly select one of them uniformly, and then another one uniformly; if one card is chosen twice, then do nothing; otherwise swap the two cards. For a number of steps, the distribution of permutations of cards stays far apart from stationarity and then it suddenly drops exponentially close to it. In this talk, I will present the similar random walk theory on compact quantum groups, and in particular present a recent analogous result in the setting of quantum random transpositions. I will also discuss the associated asymptotic description of the convergence to equilibrium, called the "cutoff profile", whose type is different from the classical examples and involves free Poisson distributions emerged from the free probability theory.

This is joint work with Amaury Freslon and Lucas Teyssier (PTRF 2022).